David Carchedi
Mathematician
My name is David Carchedi. I am Associate Professor at George Mason University. I am currently away on sabbatical at the Max Planck Institute for Mathematics (MPI) in Bonn, Germany until fall of 2026. I completed my PhD in 2011 under the supervision of Ieke Moerdijk at Utrecht University, in the Netherlands. My thesis title was "Categorical Properties of Topological and Differentiable Stacks." I was a postdoc at the MPI from 2011-2014, and afterwards a postdoc for one year at the University of British Columbia in Vancouver, Canada under the supervision of Kai Behrend before starting at GMU.
I'm proud to be a faculty mentor to GMU's chapter of the Association for Women in Mathematics (AWM). Here is a picture from the Professional Development Event for Aspiring Mathematicians
Me, Cigole Thomas (treasurer*), Ratna Khatri (president*), Marilyn Vazquez
*at time of photo
| Course | Level |
|---|---|
| N/A | ON SABBATICAL |
| Semester | Course | Level |
|---|---|---|
| Spring 2025 | Topology for Undergraduates | Undergraduate |
| Discrete Mathematics | Undergraduate | |
| Fall 2024 | Abstract Algebra | Undergraduate |
| Spring 2024 | Quantum Field Theory | Graduate (special topics) |
| Fall 2023 | Algebraic Geometry for Undergraduates | Undergraduate |
| Discrete Mathematics | Undergraduate | |
| Spring 2023 | Topology for Undergraduates | Undergraduate |
| Discrete Mathematics | Undergraduate | |
| Fall 2022 | Abstract Algebra I | Graduate |
| Discrete Mathematics | Undergraduate | |
| Spring 2022 | Abstract Algebra for Undergraduates | Undergraduate |
| Discrete Mathematics | Undergraduate | |
| Fall 2021 | Discrete Mathematics (two sections) | Undergraduate |
| Spring 2021 | Topology | Graduate |
| Introduction to Advanced Mathematics | Undergraduate | |
| Fall 2020 | Homotopy Theory | Graduate (special topics) |
| Spring 2020 | Discrete Mathematics (two sections) | Undergraduate |
| Fall 2019 | Discrete Mathematics | Undergraduate |
| Category Theory | Graduate (special topics) | |
| Spring 2018 | Moduli Spaces and Invariant Theory | Graduate (special topics) |
| Calculus II | Undergraduate | |
| Fall 2017 | Calculus II (two sections) | Undergraduate |
| Spring 2017 | Algebraic Topology | Graduate |
| Fall 2016 | Category Theory | Graduate (special topics) |
| Spring 2016 | Topology | Graduate |
| Fall 2015 | Abstract Algebra | Undergraduate |
| Semester | Course | Level |
|---|---|---|
| Spring 2015 | Calculus II | Undergraduate |
| Semester | Course | Level |
|---|---|---|
| Spring 2013 | Topos Theory | Graduate |
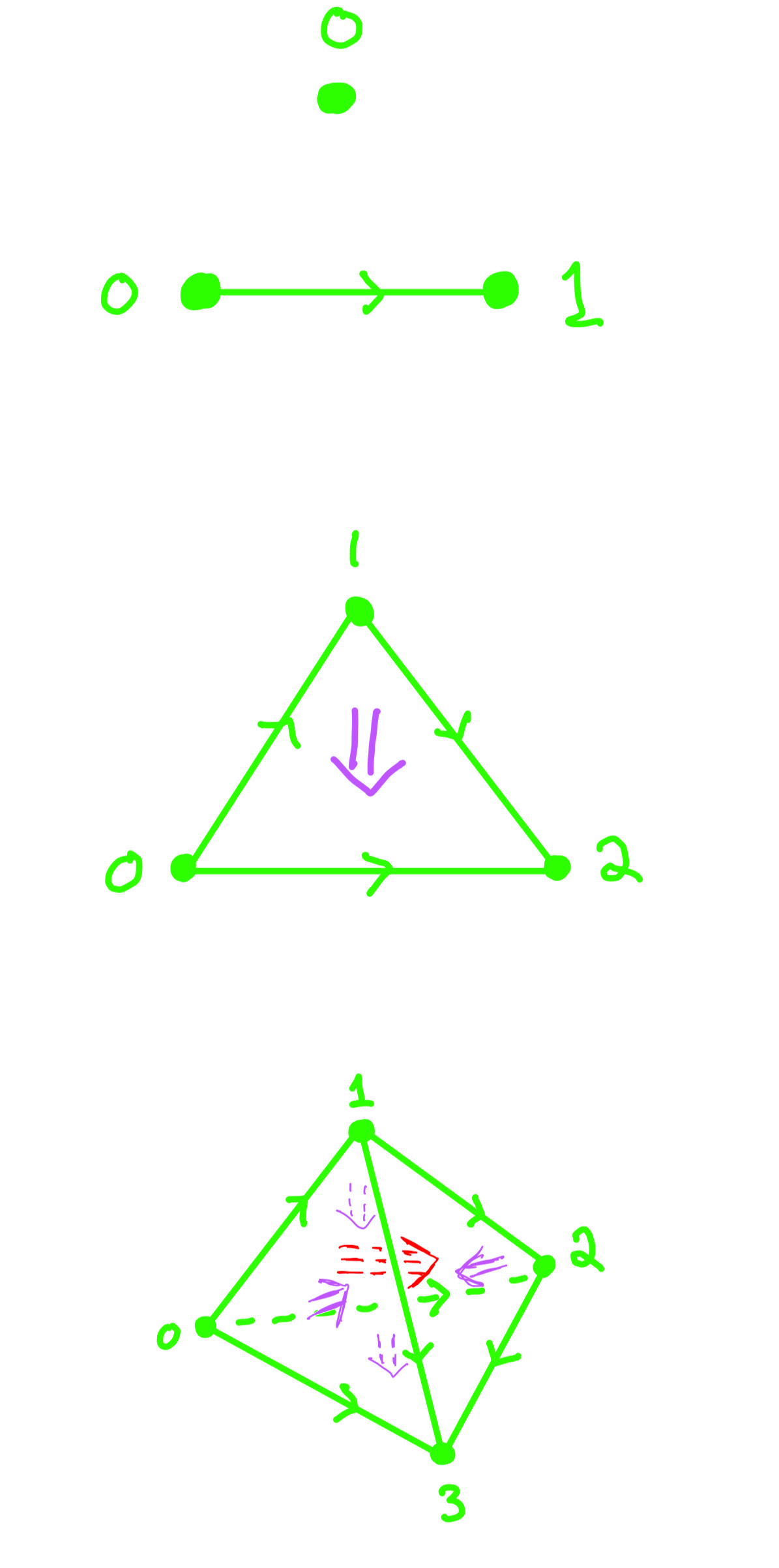
The bulk of my active research centers around developing the theory of Derived Differential Geometry (DDG) with a lens towards applications to Quantum Field Theory (QFT). Like its closely related cousin Derived Algebraic Geometry (DAG), DDG is designed to deal with non-transverse intersections. To see how non-transversality forces us out of ordinary manifolds, consider the following simple examples: The prototypical example of a transverse intersection is the \(y=x^2\) with the horizontal line \(y=1\), which has two intersection points at \(\left(-1,1\right)\) and \(\left(1,1\right)\), whereas the intersection of the same parabola with the horizontal line \(y=0\) is not transverse and has a double root. This example shows that without transversality, if we try to count roots including their multiplicities, we cannot simply count the number of points in the intersection. However, much more can go wrong than simply getting the wrong count. Indeed, if two submanifolds in an ambient manifold intersect in a non-transverse manner, the result may fail to be a manifold all together. Here is a simple example in 3D:
The idea behind derived differential geometry is to introduce derived fibered products of manifolds, which always result in a smooth object, and reduce to ordinary fibered products in the case of transversality. More formally, ordinary smooth manifolds can be realized as a subcategory of more general smooth objects, called derived manifolds, and derived fibered products are nothing but pullbacks computed in this larger category. One of the most degenerate intersection is the intersection of the origin of \(\mathbb{R}^n\) with itself, and one would hope that when computed in the category of derived manifolds, this intersection is not simply the origin, and has enough data to read off the multiplicity 2 from this example. However, this is easily seen to be impossible, as long as the one-point manifold remains a terminal object: we are computing the fibered product of \(\ast \stackrel{0}{\longrightarrow} \mathbb{R}^n\) against itself, and \(\ast\) is the terminal object. In any category \(\mathscr{C}\), any pullback of the form \(1_{\mathscr{C}} \to C\) against itself always results in the terminal object \(1_\mathscr{C}\) again. In other words, any attempt to encode multiplicities purely at the level of objects in an ordinary category fails: the universal property of pullbacks forces \(* \times_X * \simeq *\). This is not the case for higher categories however. For example, in the \(\infty\)-category of spaces, if \(\ast \stackrel{x}{\longrightarrow} X\), its pullback against itself is the based loop space \(\Omega_x\left(X\right)\). Thus, derived manifolds must form a higher category.
There have been many proposed models for what a derived manifold ought to be. The first was given by David Spivak, and Dominic Joyce has a very well-developed theory of d-manifolds, with important applications to symplectic topology. Prior to this, there was a well established tradition of the use of dg-manifolds (also called NQ-supermanifolds) in physics, spurring from the BRST,BV, and AKSZ formalisms, and work of Kontsevich.
A framework for DDG can be produced by mimicking DAG, but using an appropriate class of commutative \(\mathbb{R}\)-algebras with additional structure, called \(C^\infty\)-rings. The prototypical example of a \(C^\infty\)-ring is the ring of smooth functions on a manifold. Dmitry Roytenberg and I laid the foundations for dg-\(C^\infty\)-algebras- a differential-graded analogue of \(C^\infty\)-rings, and the resulting framework of DDG as DAG for dg-\(C^\infty\)-algebras was established by Joost Nuiten in his thesis, and further developed by Pelle Steffens, and myself. Steffens and I went on to characterize the \(\infty\)-category of derived manifolds by a universal property, and proved that the resulting \(\infty\)-category is equivalent to affine derived \(C^\infty\)-schemes of finite type . More recently, I have proven that there is an equivalent description using dg-manifolds .
There are a couple of different ways in which DDG becomes relevant in Quantum Field Theory (QFT). In classical field theory, one has a space of fields \(\mathcal{F}\) together with an action functional \(S\left(\phi\right)=\int \mathcal{L}\left(\phi\right)\), where \(\mathcal{L}\) is the Lagrangian density of the system. The dynamics of the system is governed by the solutions to the Euler-Lagrange equations, which are field configurations which are critical points for this functional. In QFT, it is not only these classical solutions which determine the physics. The system is non-deterministic and one instead extracts information by computing the expectation values of observable functions on the space of fields. Symbolically, if \(\mathcal{O}\) is an observable, the expectation value is given by: \(\langle \mathcal{O} \rangle:=\frac{1}{Z_{S,\hbar}} \underset{\phi \in \mathcal{F}} \int \mathcal{O}\left(\phi\right)e^{iS\left(\phi\right)/\hbar} \mspace{3mu}\mathcal{D}\left(\phi\right),\mspace{15mu} \mbox{ where }\mspace{15mu} Z_{S,\hbar} = \underset{\phi \in \mathcal{F}} \int e^{iS\left(\phi\right)/\hbar} \mspace{3mu}\mathcal{D}\left(\phi\right)\) is the partition function of the theory. In practice the space of fields is infinite dimensional, typically the space of sections of a fiber bundle, and there is no such measure \(\mathcal{D}\left(\phi\right)\). However, oscilliatory integrals of this form over closed manifolds, in the case that the function \(S\) in the expression \(e^{\frac{iS}{\hbar}}\) is a Morse function, can be expressed asympotically in \(\hbar\) as a sum over the set of critical points of contributions which can be neatly organized in terms of Feynman diagrams. Typically, when a physcist evaluates such a Feynman integral, they do so by computing the contributions of these Feyman diagrams. However, even in the finite dimensional case, such asymptotic expansions are only valid when the function \(S\) is Morse, or equivalently, when the Hessian \(\operatorname{Hess}\left(S\right)\) is non-degenerate. Geometrically, this is equivalent to the graph of the \(1\)-form \(dS\) being transverse to the zero section in the cotangent bundle. In essentially all physically relevant field theories however, the action functional is in fact degenerate. This has prompted sophisticated quantizations schemes which homologically resolve the action functional by adding auxilary non-physical fields as extra graded coordinates, such as the BV-BRST quantization schemes. It was through these efforts that seeds of derived geometry started to emerge in physics.
Suppose that the space of fields \(\mathcal{F}\) were in fact a closed, oriented n-manifold, and \(S\) were just a smooth function on \(\mathcal{F}\). In such a case, the integral makes sense as soon as a volume form \(\mu\) to play the role of \(\mathcal{D} \phi\) is chosen. If we choose instead \(\mu_{S,\hbar}:=e^{iS/\hbar}\cdot \mu,\) this models the path integral. Integration against this measure determines an isomorphism \(H^n\left(\mathcal{F},\mathbb{C}\right)\cong \mathbb{C}.\) Contracting with \(\mu_{S,\hbar}\) transports the de Rham differential to multi-vectorfields \(\mathfrak{X}^{\bullet}\), where it becomes a divergence operator \(\operatorname{Div}_{\mu_{S,\hbar}}.\) By construction, expectation values are just given by the class in \(H^0\left(\mathfrak{X}^{\bullet}\otimes \mathbb{C},\operatorname{Div}_{S,\mu_{\hbar}}\right).\) Moreover, \(i\hbar \cdot \operatorname{Div}_{\mu_{\hbar}} = \iota_{dS} +i \hbar \operatorname{Div}_{\mu},\) and when \(\hbar\) goes to zero, we are left with \(\left(\mathfrak{X}^{\bullet}\left(\mathcal{F}\right),\iota_{dS}\right),\) which is smooth functions on the dg-manifold \(\left(T^*\left[1\right]\mathcal{F},\iota_{dS}\right)\) which models the derived intersection of \(dS\) with the zero section. In BV language, this is precisely the object whose cohomology controls gauge-fixed observables; all the additional BV fields are a way of resolving this derived intersection.
Let \(\nabla_{BV}:=i\hbar \operatorname{Div}_{\mu_{\hbar}}.\) The complex \(\left(\mathfrak{X}^{\bullet}\otimes \mathbb{C},\nabla_{BV}\right)\) is also a graded commutative \(\mathbb{R}\)-algebra, but it fails be a dg-algebra since the divergence operator \(\nabla_{BV}\) is not a derivation for the wedge-product. Instead, one has that for multi-vector fields \(V\) and \(W\),
In this paper, we construct a refined, relative version of the étale realization functor of motivic spaces, first studied by Isaksen and Schmidt. Denoting by \(\mathcal{S}\!\operatorname{pc}\left( S \right)\) the ∞-category of motivic spaces over a base scheme \(S\), their functor goes from \(\mathcal{S}\!\operatorname{pc}\left( S \right)\) to the ∞-category of \(p\)-profinite spaces, where \(p\) is a prime which is invertible in all residue fields of \(S\).
In the first part of this paper, we refine the target of this functor to an ∞-category where \(p\)-profinite spaces is a further completion. Roughly speaking, this ∞-category is generated under cofiltered limits by those spaces whose associated "local system" on \(S\) is \(\mathbb{A}^1\)-invariant. We then construct a new, relative version of their étale realization functor which takes into account the geometry and arithmetic of the base scheme \(S\). For example, when \(S\) is the spectrum of a field \(k\), our functor lands in a certain \(\operatorname{Gal}\left(k^{\mathrm{sep}}/k\right)\)-equivariant ∞-category. Our construction relies on a relative version of étale homotopy types in the sense of Artin-Mazur-Friedlander, which we also develop in some detail, expanding on previous work of Barnea-Harpaz-Schlank.
We then stabilize our functor, in the \(S^1\)-direction, to produce an étale realization functor for motivic \(S^1\)-spectra (in other words, Nisnevich sheaves of spectra which are \(\mathbb{A}^1\)-invariant). To this end, we also develop an ∞-categorical version of the theory of profinite spectra, first explored by Quick. As an application, we refine the construction of the étale \(K\)-theory of Dwyer and Friedlander, and define its non-commutative extension. This latter invariant should be seen as an \(\ell\)-adic analog of Blanc's theory of semi-topological \(K\)-theory of non-commutative schemes. We then formulate and prove an analog of Blanc's conjecture on the torsion part of this theory, generalizing the work of Antieau and Heller.
This is the second in a series of papers laying the foundations for a differential graded approach to derived differential geometry (and other geometries in characteristic zero). In this paper, we extend the classical notion of a dg-algebra to define, in particular, the notion of a differential graded algebra in the world of \(\mathbf{C}^\infty\)-rings. The opposite of the category of differential graded \(\mathbf{C}^\infty\)-algebras contains the category of differential graded manifolds as a full subcategory. More generally, this notion of differential graded algebra makes sense for algebras over any (super) Fermat theory, and hence one also arrives at the definition of a differential graded algebra appropriate for the study of derived real and complex analytic manifolds and other variants. We go on to show that, for any super Fermat theory \(\mathbf{S}\) which admits integration, a concept we define and show is satisfied by all important examples, the category of differential graded \(\mathbf{S}\)-algebras supports a Quillen model structure naturally extending the classical one on differential graded algebras, both in the bounded and unbounded case (as well as differential superalgebras with only a \(\mathbb{Z}_2\)-grading). Finally, we show that, under the same assumptions, any of these categories of differential graded \(\mathbf{S}\)-algebras have a simplicial enrichment, compatible in a suitable sense with the model structure.
Derived geometry provides powerful tools to handle non-transverse intersections and singular moduli problems arising in geometry and theoretical physics. While derived algebraic geometry has been extensively developed, classical field theories-formulated as variational problems involving sections of smooth fiber bundles over manifolds-naturally require the language of differential geometry, infinite-dimensional analysis (e.g., Fréchet manifolds), and additional geometric structures on spacetime, such as smooth metrics. Moreover, field theories incorporating fermionic matter fields necessitate extending the framework to include supermanifolds. This article is the first in a sequence aimed at rigorously modeling the derived space of solutions to the field equations of Lagrangian gauge theories as derived \(C^\infty\)-stacks.
While this article does not explicitly discuss physics or field theory, it develops foundational aspects of derived differential geometry which are useful in their own right and contribute to the further development of the field. Moreover, these results provide essential groundwork for subsequent papers rigorously constructing derived spaces of solutions to Euler-Lagrange equations. We establish foundational results extending existing work on derived manifolds into supergeometric and infinite-dimensional contexts, and explicitly relate these constructions to differential operators and PDE theory. This paper an excerpt from a larger manuscript currently in preparation and is made available now to disseminate key foundational developments.
We begin by extending key results about derived manifolds to the supergeometric context, explicitly defining derived supermanifolds. This generalization is crucial for subsequent articles addressing fermionic matter fields. We also carefully clarify the role of infinite-dimensional manifolds in derived \(C^\infty\)-geometry, providing two different embeddings of the category of convenient manifolds of Frölicher-Kriegl-Michor into derived stacks, expanding on work of Steffens.
Moreover, we develop a novel approach to quasi-coherent sheaves, characterizing them as an explicit full subcategory of sheaves of modules on the large site. This formulation provides a concrete and explicit description of quasi-coherent sheaves over general stacks, in contrast to the traditional abstract definition as a limit of \(\infty\)-categories arising from an affine cover. It is particularly well-suited to studying examples such as de Rham stacks, which provide a natural geometric setting for analyzing PDEs. In this direction, we introduce a topos-theoretic definition of infinite jet bundles and nonlinear differential operators via the de Rham stack, and prove that this construction recovers the classical infinite jet bundle of a fiber bundle, including its Fréchet manifold structure, extending work of Khavkine-Schreiber.
Finally, we establish an equivalence between the \(\infty\)-category of quasi-coherent sheaves on the de Rham stack \(\mathcal{M}_{dR}\) of any supermanifold \(\mathcal{M}\) and the \(\infty\)-category of \(\mathcal{D}_{\mathcal{M}}\)-modules, giving a direct link to linear PDEs. Due to fundamental differences from the algebraic setting- such as the lack of compact generation, the fact that all module sheaves over affine \(C^\infty\)-schemes are quasi-coherent, and that quasi-coherent sheaves form a full subcategory of module sheaves rather than vice versa-this equivalence does not formally follow from analogous results in derived algebraic geometry.
We generalize the notion of a small sheaf of sets over a topological space or manifold to define the notion of a small stack of groupoids over an étale topological or differentiable stack. We then provide a construction analogous to the étalé space construction in this context, establishing an equivalence of 2 -categories between small stacks over an étale stack and local homeomorphisms over it. We go on to characterize small sheaves and gerbes. We show that ineffective data of étale stacks is completely described by the theory of small gerbes. Furthermore, it is shown that étale stacks (and in particular orbifolds) induce a small gerbe over their effective part, and all gerbes arise in this way. It follows that ineffective orbifolds, sometimes called non-reduced orbifolds, encode a canonical gerbe over their effective (or reduced) part. For nice enough classes of maps, for instance submersions, we show that étale stacks are equivalent to a 2 -category of gerbed effective étale stacks. Along the way, we also prove that the 2 -category of topoi is a full reflective sub-2-category of localic stacks.